PRÁTICAS EXPERIMENTAIS DE CIÊNCIAS
PERÍODO:02 A 08 DE JULHOPROFESSORA: Sandra
CONTEÚDO:Matéria e Energia: Calor e Temperatura
NÚMERO DE AULAS PREVISTAS: 2 aulas
RECURSOS:Garrafa de vidro, moeda e um pouco de água.
https://www.youtube.com/watch?v=bLerFvP-yRM
AVALIAÇÃO/SISTEMATIZAÇÃO:
Anote no caderno de prática experimental, tire foto da atividade, se for possível filme e envie a professora através do WhatsApp.
DESENVOLVIMENTO E ESTRATÉGIAS:
Leiam com atenção a atividade e assistam o Vídeo antes de
realizar o experimento.
Moeda que Pula
MATERIAL:
1. Garrafa de vidro
2. Moeda
3. Um pouco de água
1. Garrafa de vidro
2. Moeda
3. Um pouco de água
COMO
FAZER:
1. Coloque a garrafa na geladeira por quinze minutos.
2. Depois de quinze minutos, tire-a da geladeira e molhe o gargalo na água.
3. Molhe a moeda e coloque na boca da garrafa.
4. Segure a garrafa com as duas mãos.
1. Coloque a garrafa na geladeira por quinze minutos.
2. Depois de quinze minutos, tire-a da geladeira e molhe o gargalo na água.
3. Molhe a moeda e coloque na boca da garrafa.
4. Segure a garrafa com as duas mãos.
O
QUE ACONTECE:
A moeda pula.
A moeda pula.
POR QUE ACONTECE?
Resposta:Por causa do calor. Quando a gente pões a garrafa na geladeira, diminui a pressão do ar dentro dela porque a
temperatura diminuiu. O calor transmitido pelo nosso corpo aumenta a temperatura do ar de dentro da garrafa, por isso a temperatura também aumenta e empurra a moeda para cima.
DISCIPLINA; Práticas Experimentais de matemática
TURMA: 7º ANO
PROFESSOR(A): Miriam
PERÍODO: 22/06/2020 à 06/07/2020
TEMA : linguagem algébrica
HABILIDADE: AÇÃO DO MMR- compreender a ideia de variável ,representada por letra ou símbolo
Roteiro:
.
expressões matemáticas são formadas por letras
e números
Exemplo:
O
dobro de um número = 2.X ( dois vezes X)
você
chama de x o que você não conhece, que no nosso caso é um número desconhecido.
Neste caso esse X ele chama-se variável. Porque o valor dele pode ser 1, 2, 3, 4,
e assim por diante.....
Então
vamos entender essa ideia de variável ....
1) Represente
cada situação abaixo com uma sentença matemática
a) Somei um número a quinze unidades. =
b) Multipliquei um número por 4 unidades =
c) O
triplo de um número=
d) O
triplo de um número menos quarenta=
2) Guilherme
comprou uma televisão que custava x reais , mas recebeu um desconto de R$
45,00, pois pagou à vista. Qual das expressões a seguir melhor representa a
situação de Guilherme?
a) X+ 45
b) 45- X
c) X: 45
d) X-45
Agora
vamos ,fazer o seguinte....
1) Amanda
produz e vende potes de docê. Para calcular por quantos reais será vendido cada
pote, ela utiliza a fórmula V= 2,5.c + 1, em que V corresponde ao preço de
venda e c, ao custo de preparo de cada pote de doce.
a) De
acordo com a definição de variável lá em cima, leia novamente....você acha que
a letra c é uma variável ou não? Por que?
Agora
Amanda vai vender um pote de doce, se o custo de produção desse pote for R$
3,00.Por quantos reais Amanda vai vender esse pote?
A
formula é V= 2,5.c+ 1 , então fica assim...
V= 2,5.3+ 1 ( dois e meio vezes 3 mais 1)
V=7,5 + 1 ( dois e meio vezes 3 da sete e meio
então 7,5 + 1)
V= 8,5 ( sete e meio mais 1 é igual a 8,5)
Então
a resposta e V= R$ 8,50 ( valor é
igual a R$ 8,50 )
Agora
você.....
b) Se o
custo de produção desse pote for R$ 4,80. Por quantos reais Amanda vai vender
esse pote?
Elabore uma situação problema ( atividade) em que você vende ou compra alguma coisa, e tenha a (s) variáveis com a letra do seu nome.
MATERIAL DE APOIO:
Apoema
–matematica 7º ano
Vontade
de saber- matemática 7º ano
COMO SERÁ A AVALIAÇÃO:
Interação pelo whatsapp, foto da realização da atividade, entrega das
atividades e desenvolvimento.
----------------------------------------------------------------------------------------------------------------------
PRÁTICAS EXPERIMENTAIS DE CIÊNCIAS
PROFESSORA: Sandra
CONTEÚDO: Matéria e Energia: Transmissão de Calor
NÚMERO DE AULAS PREVISTAS: 2 aulas
RECURSOS:
https://www.youtube.com/watch?v=C4p0TRH6r78
AVALIAÇÃO/SISTEMATIZAÇÃO:
Após a leitura e observação da imagem, devem registrar a atividade no caderno e enviar foto para o WhaspApp, para futura verificação.
ROTEIRO
Observe uma Garrafa térmica:
Como funciona a garrafa térmica?
Garrafa térmica funciona porque suas paredes
não permitem a passagem de calor através delas conservando a temperatura do seu
conteúdo. Vamos entender como isso acontece?
Entendendo a garrafa térmica
A propagação de energia térmica se efetua por três modos diferentes: condução, convecção e radiação.
Para evitar trocas de calor por condução, a ampola interna da garrafa é feita de vidro (mau condutor) com paredes duplas, entre as quais se faz vácuo, que quase não conduz calor, já que há poucas moléculas para realizar essa tarefa.
Para isolar a garrafa das possíveis correntes de convecção (processo que ocorre com movimento de partículas), coloca-se uma tampa bem fechada.
A troca de calor por radiação é evitada espelhando as superfícies interna e externa da ampola, assim, as ondas eletromagnéticas são refletidas, tanto do conteúdo para fora como do ambiente para dentro da garrafa.
Desta maneira, a temperatura no interior da garrafa é mantida por algumas horas. O sistema não é 100% eficiente, logo, o equilíbrio térmico com o meio ambiente acontece após certo tempo. Atualmente outros materiais isolantes, como o isopor, são utilizados para conservar a temperatura de substâncias dependendo do tempo que precisam ser mantidas.
De que maneira a garrafa térmica evita transmissão
de calor por condução, convecção e irradiação?
___________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
________________________________________________________________
PRÁTICAS EXPERIMENTAIS DE MATEMÁTICA
PROFESSORA: MIRIAN
TEMA: Fração
RECURSOS:
Vontade
de saber 6º ano
Vontade
de saber 7º ano
Adaptação
de atividade pelo professor
AVALIAÇÃO/SISTEMATIZAÇÃO:
Interação pelo whatsapp, foto da realização da atividade, entrega das atividades e desenvolvimento.
AÇÃO- MMR- Realizar operações de adição e subtração de frações com denominadores diferentes.
ROTEIRO
Como
eu represento uma fração?
Exemplo:
Aqui
eu tenho quantas partes no total?
R:
12
Quantas
eu tenho pintadas?
R:
5
Então
a fração correspondente deste exemplo é 5/12- sempre o total é no denominador
(
parte de baixo da fração) e o usado, preenchido....é na parte de cima (
numerador).
Então
agora vamos adicionar e subtrair algumas frações....
Exemplo:
1/4
+ 1/4 =
2/4
Quando
os denominadores ( parte debaixo) forem
iguais eu conservo ( deixo igual) e somo somente os de cima ( numerador).
Na
subtração a mesma coisa.
Exemplo
5/4
- 3/4=2/4
Denominadores
( parte de baixo )iguais, conservo e subtraio (tiro) somente o de cima
Agora
vamos entender com denominadores diferentes....
como
eu faço?....
Acho
meu mínimo múltiplo comum (mmc) entre 4
e 3 lembra?
12 dividido por 4 deu 3 e 3 vezes 1 da 3, com a outra mesma coisa
12 dividido por 3 deu 4, e 4 vezes 1 da 4, então 3 + 4 = 7, finalizando fica 7/12.
Com a subtração mesma coisa....
Exemplo
5/12 – 1/4
acho meu mmc entre 12 e 4 deu 12, ai vai 12 dividido por 12 da 1, e 1 vezes 5 da cinco, depois 12 dividido por 4 da 3 e três vezes1 da 3, então fica 5-3 que é igual a 2/12 ou simplificando por dois dará 1/6.
Agora com vocês.....
ATIVIDADE:
a) 3/2 + 6/5=
b) 8/3 – 1/3=
c) 4/7 + 5/7=
d) 7/4 + 7/6=
e) 1/3 + 7/9 – 5/6 =
Agora para que vocês entendam melhor vamos fazer uma atividade na prática?....
Peguem 3 copos iguais. Pode ser de vidro, plástico, descartável....e vocês irão dividir ou seja fazer marcações neles assim:
No 1º copo- divida em 6 partes
iguais- faça marcas igual ao desenho, pode ser
com canetinha....lembrando que tem que ser partes iguais.
No 2º copo –divida em 3 partes
iguais- faça tambem essas marcas como no desenho- lembrando partes iguais.
No 3º copo- divida em 9 partes
iguais, igual ao desenho- lembrando que tem que ser partes iguais.
Agora vamos lá...
No primeiro copo você preenchera
com quantas partes de água?
R:
No segundo copo você
preencherá com quantas partes de água?
R:
E no terceiro você vai
despejar o copo 1 e o copo 2 .Com quantas partes vai ficar?
R:
Qual a fração do primeiro copo
?
R:
Qual a fração do segundo copo?
R:
Qual a fração do terceiro
copo?
R:
Você não despejou o copo 1 e o
2 no copo 3? Então ficará assim:
Copo 1 + copo 2 = copo 3
Monte aqui agora em forma de
fração,ou seja a fração do copo 1 mais a fração do copo 2,
faça a conta e veja o resultado . Qual foi?
R:
Agora vamos fazer a comparação....
Esta fração e equivalente a
que letra do copo 3?
R:
DICA:
Frações equivalentes são aquelas frações que correspondem ao mesmo valor numérico, isso significa que representam a mesma quantidade fracionária.
Por exemplo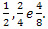 
. são iguais, já que representam a mesma quantidade.
. são iguais, já que representam a mesma quantidade.__________________________________________________________________
PRÁTICAS EXPERIMENTAIS DE CIÊNCIAS
PROFESSORA: Sandra
TEMA: CATAPULTA
Nº DE AULAS PREVISTAS: 02 aulas
RECURSOS:
https://www.youtube.com/watch?v=1Z5bNWvXl34
AVALIAÇÃO/SISTEMATIZAÇÃO:
Ao construir da sua Catapulta, você pode filmar ou tirar foto e enviar para a professora e apresentar aso retorno da aulas.
ROTEIRO
Antes da invenção dos canhões e
das armas de fogo, as catapultas eram importantes armas de guerra. Uma
catapulta era uma máquina simples, usada para lançar projéteis, ou objetos
pesados, contra um inimigo, com grande força e a grandes distâncias. Havia diversos tipos de catapultas. O mais
básico era feito de um longo braço de madeira com um grande receptáculo na
ponta. Um tubo rotatório, chamado sarilho, ficava preso a esse braço. Uma corda
era presa a ele e colocada ao redor do sarilho, dando várias voltas. Na base do
braço ficava um conjunto de cordas. Para
preparar a catapulta, os soldados apertavam a corda, girando o sarilho. Com
isso, as cordas na base do braço eram torcidas, ficando cada vez mais
apertadas. Os soldados então colocavam no receptáculo uma pedra muito grande ou
outros objetos, e depois soltavam a corda. As cordas em volta da base se
desenrolavam todas ao mesmo tempo e o braço se movia para frente, lançando sua
carga. Uma catapulta grande era capaz de arremessar uma pedra por até 460
metros de distância. As catapultas em
geral eram usadas para destruir muros de castelos. Para atacar um castelo,
normalmente era necessária mais de uma. As catapultas também eram usadas para
arremessar lanças contra um exército inimigo quando este avançava. Os exércitos
usavam catapultas grandes e pequenas. As menores eram montadas sobre rodas e
levadas para as batalhas. Carpinteiros que viajavam com os exércitos construíam
catapultas ao longo do percurso até as batalhas. As de grande porte geralmente
ficavam em um só lugar e eram usadas pelos moradores das cidades e dos castelos
para se defender. As primeiras
catapultas surgiram no século
XIII a.C. Os romanos da Antiguidade aprimoraram o artefato e construíram catapultas sobre rodas. Os exércitos de hoje usam equipamentos
baseados na catapulta para lançar mísseis e aviões.
Mão
na Massa
✓
Realizar uma construção de uma Catapulta:
✓ Materiais necessários: palitos de sorvete, palitos de dente, espeto
de churrasco, colheres de plástico, copo plástico (normal e de café), tampinha
de refrigerante ou suco, tesoura ou estilete, fita adesiva, elástico de
borracha, cola branca, cola quente, papelão, canetinhas, objetos pequenos a
serem disparados.
Questões:
1). Qual é o princípio básico de funcionamento da
catapulta?
2). Quais tipos de catapulta você conseguiu construir?
3). Teve alguma que não funcionou como esperado? Consegue
propor alguma ideia?
4). Que melhoria/adaptação você acha que poderia fazer no
seu projeto?
Sem comentários:
Enviar um comentário